The Spherical Harmonic (SH) series has proved itself a useful mathematical tool in various domains like quantum mechanics and acoustics, as well as in lighting computations.
However the traditional definition from quantum mechanics (other variations exist) is somewhat intimidating:
![Rendered by QuickLaTeX.com \[ Y_{\ell }^{m}(\theta ,\varphi )=(-1)^{m}{\sqrt {{(2\ell +1) \over 4\pi }{(\ell -m)! \over (\ell +m)!}}}\,P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi } \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-fc512261f6894369c31f82ad70e344be_l3.png)
The constants here are well-motivated: they are required so that quantum mechanical probability distributions are normalised to 1… but if we blindly plug this definition straight in for a 3D graphics/lighting use case, we end up evaluating lots of trigonometric functions and carrying around complicated factors of 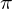 that aren’t necessary. In the literature, these constants are often quoted as decimal quantities without explanation, making everything even more confusing. If instead we make a simplifying redefinition, our SH coefficients become easier to interpret and the computations require no trigonometry and fewer magic constants (and thus, hopefully, less debugging…)
that aren’t necessary. In the literature, these constants are often quoted as decimal quantities without explanation, making everything even more confusing. If instead we make a simplifying redefinition, our SH coefficients become easier to interpret and the computations require no trigonometry and fewer magic constants (and thus, hopefully, less debugging…)
Background
The Spherical Harmonic (SH) series of functions is the analogue of the Fourier Series for functions on the surface of a 2-sphere 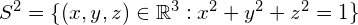 . The complete set of functions is an infinite-dimensional basis for functions on the sphere, but in practical use the series is truncated to give an approximation of an arbitrary function by a finite weighted sum of basis functions.
. The complete set of functions is an infinite-dimensional basis for functions on the sphere, but in practical use the series is truncated to give an approximation of an arbitrary function by a finite weighted sum of basis functions.
In computer graphics, spherical harmonics are used as a form of compression, which in turn greatly accelerates computations. For instance, the incoming light at a point in space is a spherical function (since it varies with direction), but using SH its approximation can be compactly represented by a handful of coefficients (the weights for the first few basis functions). This allows computations to be performed on a vector of these SH coefficients, rather than the spherical functions themselves.
Spherical harmonics are a good choice for this compressed representation because the SH approximation is invariant under rotation. That is, the SH approximation of a rotated function is the same as the rotated SH approximation of the original function.
Spherical Harmonic Bands
The Spherical Harmonic series is composed of separate “bands” of functions, usually denoted L0, L1, L2 etc. The L0 band is a single constant function; the L1 band consists of three linear functions; the L2 band contains five quadratic functions; and so on. For real-time lighting it is unusual to go past the L2 band (which requires nine total coefficients per channel) since the data and computation requirements become large, and the L2 approximation is already pretty accurate. However use cases in physics and astronomy can require up to L3000!
We will return to the bands later, but for now let’s start with some definitions.
Truncated Weighted Sum
Given a basis 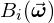 , a spherical function
, a spherical function 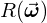 can be written as a weighted sum:
can be written as a weighted sum:
![Rendered by QuickLaTeX.com \[ R(\vec{\boldsymbol{\omega}}) = R_0 B_0(\vec{\boldsymbol{\omega}}) + R_1 B_1(\vec{\boldsymbol{\omega}}) + R_2 B_2(\vec{\boldsymbol{\omega}}) + \ldots \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-ff3c8230322a765784d6c22012388567_l3.png)
where 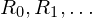 are scalar coefficients.
are scalar coefficients.
Truncating the sum gives a finite approximation:
![Rendered by QuickLaTeX.com \[ R_{tr}(\vec{\boldsymbol{\omega}}) \, = \, R_0 B_0(\vec{\boldsymbol{\omega}}) + \ldots + R_n B_n(\vec{\boldsymbol{\omega}}) \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-1348809f467f276d8fa21362ab4f39f9_l3.png)
where the vector of coefficients  fully describes the approximation.
fully describes the approximation.
Standard Inner Product
Recall that the standard definition of the inner product of spherical functions 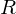 ,
, 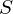 is a spherical integral:
is a spherical integral:
![Rendered by QuickLaTeX.com \[ \langle R, S \rangle_{std} = \oint \, R(\vec{\boldsymbol{\omega}}) \, S(\vec{\boldsymbol{\omega}}) \, d\Omega \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-99fd9840e0c21de8da7ac8c5000dcf1b_l3.png)
where 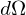 is the measure over the sphere and
is the measure over the sphere and 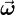 is the variable of integration.
is the variable of integration.
Therefore if the basis is orthogonal we compute the coefficients for a function with integrals:
![Rendered by QuickLaTeX.com \[ R_i = \langle R, B_i \rangle_{std} = \oint \, R(\vec{\boldsymbol{\omega}}) \, B_i(\vec{\boldsymbol{\omega}}) \, d\Omega \quad \quad i = 0, 1, \ldots \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-7bc5caf0ad5095b0852ad146706fa981_l3.png)
Constant Basis Function
The standard definition of the first SH basis function — the single function in L0 — is:
![Rendered by QuickLaTeX.com \[ Y_0^0 (\vec{\boldsymbol{\omega}}) = \frac{1}{\sqrt{4\pi}} \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-4c67d3fc808e07dd888f106a5c3e236f_l3.png)
This defintion is motivated by ensuring normalisation over the sphere, that is:
![Rendered by QuickLaTeX.com \[ \langle Y_0^0, Y_0^0 \rangle_{std} \, = \, \oint (Y_0^0)^2 \, d\Omega \, = \, \oint \frac{1}{4\pi} \, d\Omega \, = \, 1 \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-4846338e76d4fc9d07230f964b6fb6e4_l3.png)
However for our use case this “extra” factor of 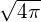 is redundant. Consider what happens when we approximate a constant function
is redundant. Consider what happens when we approximate a constant function  . First we compute the first SH coefficient:
. First we compute the first SH coefficient:
![Rendered by QuickLaTeX.com \[ R_0 = \oint R(\vec{\boldsymbol{\omega}}) Y_0^0 d\Omega =\oint \alpha \frac{1}{\sqrt{4 \pi}} d\Omega = \sqrt{4\pi} \alpha \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-8d4fb363148cf21782475d0a19e3d246_l3.png)
Now to construct the SH approximation we form the weighted sum of basis functions, that is we multiply the coefficient and the basis function:
![Rendered by QuickLaTeX.com \[ R_{sh}(\vec{\boldsymbol{\omega}}) = R_0 Y_0^0 = \frac{\sqrt{4\pi}\alpha }{\sqrt{4\pi}} = \alpha \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-8c51785a54f8385481ffa8b4bcc250f7_l3.png)
As expected, the function is reconstructed exactly, but the process is clearly more complicated than necessary: we gain a factor of 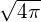 in the SH coefficient only to cancel it with the same factor in the basis function.
in the SH coefficient only to cancel it with the same factor in the basis function.
The factor of 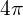 arises since it is the surface area of the unit sphere, but that isn’t relevant to our intended use case. It is much simpler to subsume this factor in a new definition of the inner product.
arises since it is the surface area of the unit sphere, but that isn’t relevant to our intended use case. It is much simpler to subsume this factor in a new definition of the inner product.
Normalised Inner Product
Redefine the inner product:
![Rendered by QuickLaTeX.com \[ \langle R, S \rangle \, = \, \frac{1}{4\pi} \oint R(\vec{\boldsymbol{\omega}}) \, S(\vec{\boldsymbol{\omega}}) \, d\Omega \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-7c38615c7561ad2d1cd8953fe28d96c5_l3.png)
The idea is to “normalise so the surface area of the sphere is one.” With this new definition, for  we now obtain the more natural outcome that the corresponding SH coefficient
we now obtain the more natural outcome that the corresponding SH coefficient 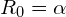 .
.
In fact this definition results in a 1-to-1 correspondence between the constructive approach of computing SH coefficients via sampling and the theoretical integral form:
![Rendered by QuickLaTeX.com \[ R_0 = \frac{1}{n} \sum_{i=1}^{n} R(\vec{\boldsymbol{\omega}}_i) \quad \mapsto \quad R_0 = \frac{1}{4\pi} \oint R(\vec{\boldsymbol{\omega}}) \, d\Omega \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-80dfa443d7a618bf08af8fb3eb5c7496_l3.png)
where 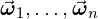 are samples taken from a uniform spherical distribution.
are samples taken from a uniform spherical distribution.
This means that to compute the 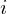 th SH coefficient we simply sum the values of the
th SH coefficient we simply sum the values of the 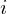 th basis function for
th basis function for 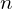 given sample directions and divide the result by
given sample directions and divide the result by 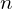 .
.
Notation
We will abuse the notation 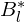 for the basis functions, where the subscript
for the basis functions, where the subscript 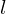 is the band, and the superscript is an index within the band. This is the similar to the standard notation, except that we use
is the band, and the superscript is an index within the band. This is the similar to the standard notation, except that we use 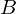 rather than
rather than 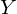 to distinguish our renormalised basis functions.
to distinguish our renormalised basis functions.
L0 Band
With our renormalised inner product, we can define the first SH basis function:
![Rendered by QuickLaTeX.com \[ B_0^0 (\vec{\boldsymbol{\omega}}) = 1 \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-ade2ae56711e4b63332945e836c6635c_l3.png)
This is the only basis function which has a non-zero average value over the sphere. This means that the first SH coefficient for a function represents the average energy over the sphere — the subsequent coefficients and basis functions neither add nor remove energy (instead they simply “move it around”).
L1 Band
Define:
![Rendered by QuickLaTeX.com \[ B_1^{-1,0,1} = x, y, z \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-fd6493688cdc4563227dbcd8ff2a547b_l3.png)
Note that we have chosen functions which are not unit-length with respect to our inner product. This is deliberate. We choose to take care of the normalisation in the reconstruction step — that is, when we compute the approximation 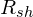 . If the function we are measuring is radiance (incoming light) then for shading we need to convert it to irradiance (outgoing light) for a given normal direction, and the reconstruction coefficients will get swept into this conversion.
. If the function we are measuring is radiance (incoming light) then for shading we need to convert it to irradiance (outgoing light) for a given normal direction, and the reconstruction coefficients will get swept into this conversion.
In fact, it is convenient to think of the L1 band as a single vector 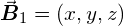 with corresponding SH coefficients
with corresponding SH coefficients 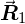 .
.
The direction of 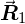 is the average direction of the function
is the average direction of the function 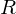 . If
. If 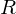 is radiance, then it is the average direction of the incoming light (weighted by intensity).
is radiance, then it is the average direction of the incoming light (weighted by intensity).
By construction, the length of 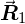 will vary between zero and
will vary between zero and 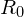 , the first SH coefficient. The ratio
, the first SH coefficient. The ratio 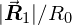 is an indication of “how directional” the function is. If the ratio is one then
is an indication of “how directional” the function is. If the ratio is one then 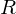 is completely directional — all of the energy is at a single point on the sphere. Conversely, if the ratio is zero then
is completely directional — all of the energy is at a single point on the sphere. Conversely, if the ratio is zero then 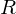 is symmetrical, and the L1 band gives us no directional information at all.
is symmetrical, and the L1 band gives us no directional information at all.
L2 Band
There are six different quadratic combinations of the variables 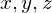 :
:
![Rendered by QuickLaTeX.com \[ x^2, y^2, z^2, xy, yz, xz \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-3304ab792bf340f4c913b63c19ab9bc2_l3.png)
However, since we are on the surface of a 2-sphere we know that 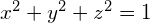 . Therefore there is one linear dependency between these six functions, and we end up with five basis functions in L2.
. Therefore there is one linear dependency between these six functions, and we end up with five basis functions in L2.
The simplest way to capture the L2 band is a 3×3 matrix:
![Rendered by QuickLaTeX.com \[ B_2^{ij} = \omega _i \omega _j - \tfrac{1}{3} \delta _{ij} \quad \quad \quad i, j \in \{1,2,3\} \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-50652a4ed39a804edbc9fa68af2dacf9_l3.png)
with a corresponding matrix 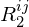 of SH coefficients, where
of SH coefficients, where 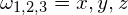 and
and 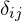 is one if
is one if 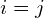 and zero otherwise. The negative one-third term is required to ensure each function has zero integral over the sphere, so is orthogonal to the constant basis function.
and zero otherwise. The negative one-third term is required to ensure each function has zero integral over the sphere, so is orthogonal to the constant basis function.
This 3×3 matrix 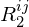 is symmetric, meaning that
is symmetric, meaning that 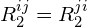 , and traceless, meaning that the diagonal elements sum to zero:
, and traceless, meaning that the diagonal elements sum to zero: 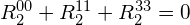 . Therefore it does indeed have five degrees of freedom (and an actual implementation would not store nine coefficients!)
. Therefore it does indeed have five degrees of freedom (and an actual implementation would not store nine coefficients!)
Whereas L0 and L1 have relatively simple physical meanings, it is harder to grasp L2 intuitively. The linear L1 band is “antipodal” in the sense that if you add weight in the 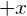 direction then it must be balanced by negative weight in the opposite
direction then it must be balanced by negative weight in the opposite  direction. For the quadratic L2 band, the
direction. For the quadratic L2 band, the 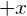 and
and  directions are the same (since their squares are equal). Instead, to ensure a net-zero overall contribution, if weight is added to the
directions are the same (since their squares are equal). Instead, to ensure a net-zero overall contribution, if weight is added to the 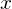 axis then the balancing negative weight is shared equally in the orthogonal
axis then the balancing negative weight is shared equally in the orthogonal 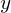 and
and 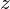 axes.
axes.
Although L2 is already a good approximation, in the case of CG lighting this property can have counter-intuitive effects: adding a light may cause “negative light” to appear in some orthogonal direction.
Reconstruction
With the above definitions, the SH approximation to the original function is:
![Rendered by QuickLaTeX.com \[ R_{sh}(\vec{\boldsymbol{\omega}}) = R_0 + 3 \vec{\boldsymbol{R}}_1 \! \cdot \! \vec{\boldsymbol{\omega}} + \tfrac{15}{2}\omega_i \omega_j R_2^{ij} + \ldots \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-f38e7cd87de752389d345d124f412b16_l3.png)
This formulation requires only simple rational constants applied in the reconstruction step.
Conclusion
Everything should be made as simple as possible, but no simpler.
Albert Einstein
We have shown how to redefine the SH basis functions for L0, L1 and L2 in a way that is simpler and more natural for many use cases. This definition removes all trigonometric functions, factors of 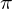 and square roots, and just leaves the rational constants required for normalisation. The process can be naturally extended to higher SH bands as required.
and square roots, and just leaves the rational constants required for normalisation. The process can be naturally extended to higher SH bands as required.
Although we’ve mentioned lighting a few times in this post, nothing here is lighting-specific. In the next post we’ll discuss a lighting problem: how best to convert from SH radiance (incoming light) to irradiance (outgoing light).
![]() :
:![]()
![]()
![Rendered by QuickLaTeX.com \[ =\frac{1}{4}\left( \frac{1}{\pi} \int_{H+}\vec{\boldsymbol{n}}\!\cdot\!\vec{\boldsymbol{\omega}}\, R(\vec{\boldsymbol{\omega}}) \, d\Omega +\frac{1}{\pi}\int_{H-}\vec{\boldsymbol{n}}\!\cdot\!\vec{\boldsymbol{\omega}}\, R(\vec{\boldsymbol{\omega}}) \, d\Omega \right) \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-f8073d3ab4c779eb128488c89b65b57b_l3.png)
![]()
![Rendered by QuickLaTeX.com \[ I(\vec{\boldsymbol{n}}) = \begin{cases} 4 (\vec{\boldsymbol{d}} . \vec{\boldsymbol{n}}) & \text{if}\ \vec{\boldsymbol{d}} . \vec{\boldsymbol{n}} \ge 0 \\ 0 & \text{otherwise} \end{cases} \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-2e34ad873e469d7b70cf68033bcac2e6_l3.png)
![Rendered by QuickLaTeX.com \[ p = 1 + 2 \frac{| \vec{\boldsymbol{R}}_1 |}{R_0} \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-e6b45e4e36c968a48bf725a94d3d67e2_l3.png)
![Rendered by QuickLaTeX.com \[ a = (1 - \frac{|\vec{\boldsymbol{R}}_1 |}{R_0}) / (1 + \frac{|\vec{\boldsymbol{R}}_1 |}{R_0}) \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-860d271bdf9edd6045d82597c4ff8ee8_l3.png)
![Rendered by QuickLaTeX.com \[ Y_{\ell }^{m}(\theta ,\varphi )=(-1)^{m}{\sqrt {{(2\ell +1) \over 4\pi }{(\ell -m)! \over (\ell +m)!}}}\,P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi } \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-fc512261f6894369c31f82ad70e344be_l3.png)
![Rendered by QuickLaTeX.com \[ Y_0^0 (\vec{\boldsymbol{\omega}}) = \frac{1}{\sqrt{4\pi}} \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-4c67d3fc808e07dd888f106a5c3e236f_l3.png)
![Rendered by QuickLaTeX.com \[ R_0 = \oint R(\vec{\boldsymbol{\omega}}) Y_0^0 d\Omega =\oint \alpha \frac{1}{\sqrt{4 \pi}} d\Omega = \sqrt{4\pi} \alpha \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-8d4fb363148cf21782475d0a19e3d246_l3.png)
![Rendered by QuickLaTeX.com \[ R_{sh}(\vec{\boldsymbol{\omega}}) = R_0 Y_0^0 = \frac{\sqrt{4\pi}\alpha }{\sqrt{4\pi}} = \alpha \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-8c51785a54f8385481ffa8b4bcc250f7_l3.png)
![Rendered by QuickLaTeX.com \[ R_0 = \frac{1}{n} \sum_{i=1}^{n} R(\vec{\boldsymbol{\omega}}_i) \quad \mapsto \quad R_0 = \frac{1}{4\pi} \oint R(\vec{\boldsymbol{\omega}}) \, d\Omega \]](https://grahamhazel.com/blog/wp-content/ql-cache/quicklatex.com-80dfa443d7a618bf08af8fb3eb5c7496_l3.png)